Construções Geométricas

Quando alguém vai construir uma casa, ela não pode apenas ficar colocando tijolos sem pensar no que está fazendo. Ela precisa imaginar ela pronta, pensar em suas características, para depois construir. O mesmo vale aqui. Em problemas de construções geométricas, você deve imaginar a construção pronta e ver quais propriedades são interessantes e você consegue desenhar.

Existem construções bem conhecidas que durante as soluções não precisam ser explicadas e nem detalhadas, mas que você deve saber para resolver problemas, como por exemplo:

Exemplo[]

Construa um triângulo dado um ângulo, a altura relativa ao vértice do ângulo dado e o perímetro do triângulo.

Solução: Vamos nomear os objetos principais do problema. Seja $ABC$ o triângulo, de forma que $\angle BAC = \alpha$ seja o ângulo dado. Considere $\ h$ a altura relativa a esse ângulo e $\ p$ o perímetro da figura.

Também consideraremos $a=BC$ , $b=CA$ e $c=AB$ . A questão é: como podemos usar cada uma das informações do enunciado? Para fazermos aparecer um ângulo, basta construirmos um arco capaz. Para fazermos a altura $\ h$ , basta sabermos construir uma reta paralela com distância igual a $\ h$ (uma maneira de fazermos isso é traçarmos duas retas perpendiculares e marcarmos em cada uma um ponto de distância $\ h$ da reta que queremos considerar).

Mas o que fica mais problemático aqui é: como podemos fazer para usar o perímetro? Existem várias formas de se fazer isso. Precisamos pensar em um critério para escolher qual é a mais vantajosa. Vamos imaginar a figura pronta.

Colocamos na nossa figura o ângulo e altura. Mas ainda não colocamos o perímetro. A questão é: onde colocar? Como o perímetro é a soma dos lados, vale a pena colocar em cima de alguns lados (por exemplo, se colocarmos em cima do lado que mede $\ a$ devemos prolongar o segmento de forma a aumentarmos ele na medida $b + c$ ). A questão é: sobre qual lado devemos colocar esse perímetro?

Se colocarmos ele sobre o lado $AB$ funciona? O quão isso seria coerente com os dados do problema? Pense no seguinte: o problema é simétrico em relação aos lados $\ b$ e $\ c$ (ou seja, se trocarmos esses lados, o problema continuaria o mesmo). Colocar conforme a figura acima não usa essa simetria. Como podemos usá-la então? Uma maneira é colocarmos o perímetro sobre o lado $BC$ .

Mas qual lado prolongar esse segmento? Se prolongarmos somente para um lado, não estaremos aproveitando a simetria dele. Então vale a pena prolongarmos para os dois lados: medida $\ b$ para um lado e medida $\ c$ para o outro. Porém, em qual lado colocar a medida $\ b$ e qual lado colocar medida $\ c$ . Lembre-se: ao introduzir elementos auxiliares, procure fazer isso de forma que você ganhe boas propriedades. Se você colocar conforme a figura a seguir, acabará ganhando dois triângulos isósceles.

Observe que $DE=a+b+c=p$ . Para ganharmos os triângulos isósceles, precisamos ligar $\ D$ com $\ A$ e $\ E$ com $\ A$ .

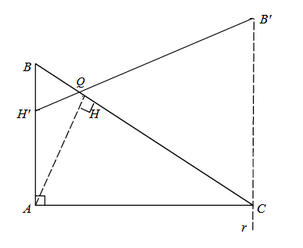
Ou seja, podemos começar a nossa figura com os pontos $\ D$ e $\ E$ , pois já ganhamos o polígono com isso. Só restaria encontrarmos as posições de $\ A$ , $\ B$ e $\ C$ . Como podemos começar construindo $\ A$ ? Já temos uma característica dele: ele está a uma distância $\ h$ de $DE$ , ou seja, precisaríamos construir uma reta paralela com distância $\ h$ . Mas só isso não basta. Precisamos de outra característica de $\ A$ em função de $\ D$ e $\ E$ .

Uma ideia aqui seria calcularmos a medida de $\angle DAE$ , pois se ela depender apenas de $\alpha$ podemos determinar esse ângulo e construir seu arco capaz. Considere $\angle ABC = \beta$ e $\angle ACB=\gamma$ . Observe que $\angle ABC$ é externo ao triângulo $ABD$ que é isósceles de base $AD$ . Desta forma, $\angle DAB={\frac {\beta }{2}}$ . Analogamente, $\angle CAB={\frac {\gamma }{2}}$ . Como $\angle BAC = \alpha$ , segue que

$\angle DAE=\alpha +{\frac {\beta +\gamma }{2}}.(*)$

Para escrevermos $\angle DAE$ em função de $\ \alpha$ , precisamos escrever $\beta+\gamma$ em função de $\ \alpha$ . Como a soma dos ângulos internos do triângulo $ABC$ é $180^{\circ}$ , segue que $\alpha+ \beta+ \gamma = 180^\circ$ , ou seja, $\beta +\gamma =180^{\circ }-\alpha$ . Ao substituirmos em $(*)$ ,

$\angle DAE=\alpha +{\frac {180^{\circ }-\alpha }{2}}=90^{\circ }+{\frac {\alpha }{2}}.$

Para construimos $\ A$ , basta construirmos o arco capaz de $90^{\circ }+{\frac {\alpha }{2}}$ (para termos esse ângulo, basta construirmos a bissetriz de $\ \alpha$ e adicionarmos com um ângulo de $90^\circ$ ) e vermos onde se intersecta com a reta paralela de distância $\ h$ de $DE$ (pode ser em mais de um ponto). Agora, resta construirmos os pontos $\ B$ e $\ C$ .

Já sabemos que ambos os pontos estão sobre $DE$ . Precisamos de outra característica deles. Observe que $BD=BA$ e assim $\ B$ está na mediatriz de $AD$ . Logo, basta traçarmos esse mediatriz e vermos onde ela se encontra com $DE$ para construirmos o ponto $\ B$ . A construção de $\ C$ é análoga.

Exemplo (Cone Sul 2002)[]

De um triângulo $ABC$ , retângulo em $A$ , conhecemos: o ponto $T$ de tangência da circunferência inscrita em $ABC$ com a hipotenusa $BC$ , o ponto $D$ de interseção da bissetriz interna do ângulo $\angle B$ com o lado $AC$ e $E$ de interseção da bissetriz interna do ângulo $\angle C$ com o lado $AB$ . Descreva uma construção com régua e compasso para obter os pontos $A, B$ e $C$ . Justifique.

Solução: Em outras palavras, precisamos construir $A$ , $B$ e $C$ a partir dos pontos $T$ , $D$ e $E$ . Vamos imaginar a construção pronta.

Como podemos relacionar $D$ e $E$ com os outros vértices? Sabemos que os pontos da bissetriz são equidistantes aos outros vértices. Desta maneira, se $W$ e $Y$ são pontos de $BC$ tais que $DW$ e $EY$ são perpendiculares a $BC$ , segue que $AD=DW$ e $AE=EY$ .

Qual a vantagem disto? É que $A$ pertence à circunferência de centro $E$ e raio $EY$ e também à de centro $D$ e raio $DW$ . Com isso, podemos construir $A$ a partir de $D$ , $E$ , $W$ e $Y$ .

Mas como construimos $W$ e $Y$ a partir de $D$ e $E$ ? Para isto, precisamos da reta $BC$ . Detalhe: eu disse reta e não segmento.

Observe que ainda não usamos o ponto $T$ . Como podemos relacioná-los com o resto da figura? Que tal calcularmos $WT$ e $TY$ para ver se descobrimos algo?

Vamos considerar algumas medidas. Sejam $a=BC$ , $b=AC$ , $c=AB$ e $p$ o semiperímetro do triângulo $ABC$ . Uma das maneiras de calcularmos $WT$ é sabermos $WB$ e $TB$ e depois subtrairmos.

Como $T$ é ponto de tangência, segue que $TB=p-b$ . E quanto a $WB$ ? Como os triângulos $ABD$ e $WBD$ são congruentes, segue que $WB=AB=c$ . Desta forma,

$WT=WB-TB=c-(p-b)=p-a.$

Da mesma forma, para calcularmos $YT$ , precisamos calcular $YC$ e $CT$ e subtrair um do outro. E de modo análogo, podemos ver $YC=b$ e $CT=p-a$ . Desta forma,

$YT=YC-CT=b-(p-c)=p-a.$

Assim $WT=TY$ , ou seja, $T$ é ponto médio de $WY$ . Considere $N$ o ponto médio do segmento $DE$ . Qual a vantagem disto? É que $NT$ é base média do trapézio $DEWY$ , de onde segue que $NT$ é perpendicular a $BC$ .

A partir de agora podemos construir a reta $BC$ . De fato, tome um ponto $N'$ sobre a reta $NT$ de forma que $TN'=TN$ . Observe que a mediatriz de $NN'$ coincide com a reta $BC$ .

Agora sim podemos construir $W$ e $Y$ a partir de $D$ , $E$ e $T$ : basta construirmos a reta $BC$ e depois tomarmos $W$ e $Y$ sobre a reta $BC$ de forma que $DW$ e $EY$ são perpendiculares a $BC$ .

Agora já temos condições de construirmos $A$ : basta tomarmos um dos pontos de intersecção entre a circunferência de centro $D$ e raio $DW$ e a de centro $E$ e raio $EY$ .

E como construimos $B$ e $C$ em termos do que já temos construído? Basta considerarmos os pontos de intersecção da mediatriz de $NN'$ com $AE$ e $AD$ e teremos, respectivamente, $B$ e $C$ . Com isso, teremos o triângulo $ABC$ .

Mas quem garante que $W$ ou $Y$ não coincidam com $T$ ? Se isso $W$ coincidisse com $T$ , então $WT=p-a=0$ , ou seja, $a=b+c$ , o que contradiz a Desigualdade Triangular. Pelo mesmo motivo, $Y$ também não pode coincidir com $T$ .

Construção:

(1) Considere $N$ o ponto médio de $DE$ .

(2) Tome $N'$ um ponto sobre a reta $NT$ tal que $NT=TN'$ .

(3) Construa a mediatriz de $NN'$ .

(4) Considere construa perpendiculares à mediatriz de $NN'$ passando por $D$ e $E$ . Os pontos de intersecção com a mediatriz de $NN'$ , chame de $W$ e $Y$ , respectivamente.

(5) Tome $B$ e $C$ os pontos de intersecção da mediatriz de $NN'$ com $AE$ e $AD$ , respectivamente.

Construa Pontos Usando Razões[]

Considere $AB$ um segmento e dois pontos $C$ e $D$ pertencentes a ele. Se ${\frac {AC}{CB}}={\frac {AD}{DB}}$ , então $C$ e $D$ coincidem.

Às vezes, para construir $C$ , precisamos encontrar um ponto $D$ tal que ${\frac {AC}{CB}}={\frac {AD}{DB}}$ .

Exemplo (Cone Sul 1999)[]

Seja $ABC$ um triângulo retângulo em $A$ . Construir o ponto $P$ sobre a hipotenusa $BC$ , tal que se $Q$ for o pé da perpendicular traçada desde $P$ ao cateto $AC$ , então a área do quadrado de lado $PQ$ é igual à área do retângulo de lados iguais a $PB$ e $PC$ . Mostrar os passos da construção.

Solução: Em outras palavras, queremos que $PQ^{2}=PB.PC(*)$ . A ideia aqui é calcularmos ${\frac {PB}{PC}}$ em função de elementos do triângulo $ABC$ e depois conseguirmos construir um ponto $Q$ pertencente a $BC$ tal que ${\frac {QB}{QC}}={\frac {PB}{PC}}$ .

Vamos imaginar a construção pronta. Encontraremos relações que envolvam $PQ,PB$ e $PC$ para depois podermos comparar com $(*)$ .

Conseguimos envolver $PQ$ e $PC$ em uma semelhança agora. Com efeito, observe que $PQ$ é paralelo a $AB$ de onde segue que $PQC$ e $BAC$ são semelhantes. Com isso,

${\frac {PQ}{AB}}={\frac {PC}{BC}}\Leftrightarrow PQ={\frac {PC.AB}{BC}}.$

Se substituirmos em $(*)$ :

$\left({\frac {PC.AB}{BC}}\right)^{2}=PB.PC\Leftrightarrow {\frac {AB^{2}}{BC^{2}}}={\frac {PB}{PC}}.(**)$

Também conseguimos calcular $AB^2$ de outra maneira. De fato, se $AH$ for a altura relativa a $BC$ , então

$AB^{2}=BH.BC$

Se substituirmos em $(**)$ :

${\frac {BH.BC}{BC^{2}}}={\frac {PB}{PC}}\Leftrightarrow {\frac {BH}{BC}}={\frac {PB}{PC}}.$

Construiremos um ponto $Q$ pertencente a $BC$ tal que ${\frac {QB}{QC}}={\frac {BH}{BC}}(***)$ . Se isto acontecer, teremos construído o ponto $P$ .

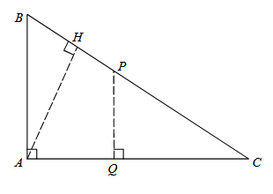
Como aparecem razões, é interessante que consigamos uma semelhança que envolva $QB$ , $QC$ , $BH$ e $BC$ . Para encontrarmos essa semelhança, tomemos algum paralelismo. Faremos isto da seguinte maneira: tomaremos $B'$ um ponto tal que $B'C$ é paralelo a $BC$ . Ainda precisamos da medida de $B'C$ para determinarmos exatamente a sua maneira de construir. Faremos isto depois.

Além disso, tomemos $H'$ o ponto de intersecção entre $AB$ e $B'Q$ (lembre-se que depois precisamos determinar a medida de $BH'$ para podermos saber qual a posição exata de $Q$ ). Qual a vantagem de fazermos isto? É que conseguimos que $QBH'$ e $QCB'$ são semelhantes. Desta semelhança,